The diffusion model describes how infected individuals spread an infection to susceptible individuals. Alternatively, it describes the adoption of a product or technology as adopters influence potential adopters through word of mouth. I will refer to it as the SI model, based on the first scenario, Figure 1.

The model has two loops, and the impacts of the loops show shifting loop dominance from the reinforcing loop, R1 to the balancing loop. Read Diffusion Model for this analysis. In the Newtonian Interpretative Framework, feedback loops are viewed as forces, measured by loop impact. As forces, the loops do work on the stocks. Reinforcing loops inject dynamic energy into stocks, making them change faster. By contrast, balancing loops remove energy, slowing down their change.
Kinetic Energy
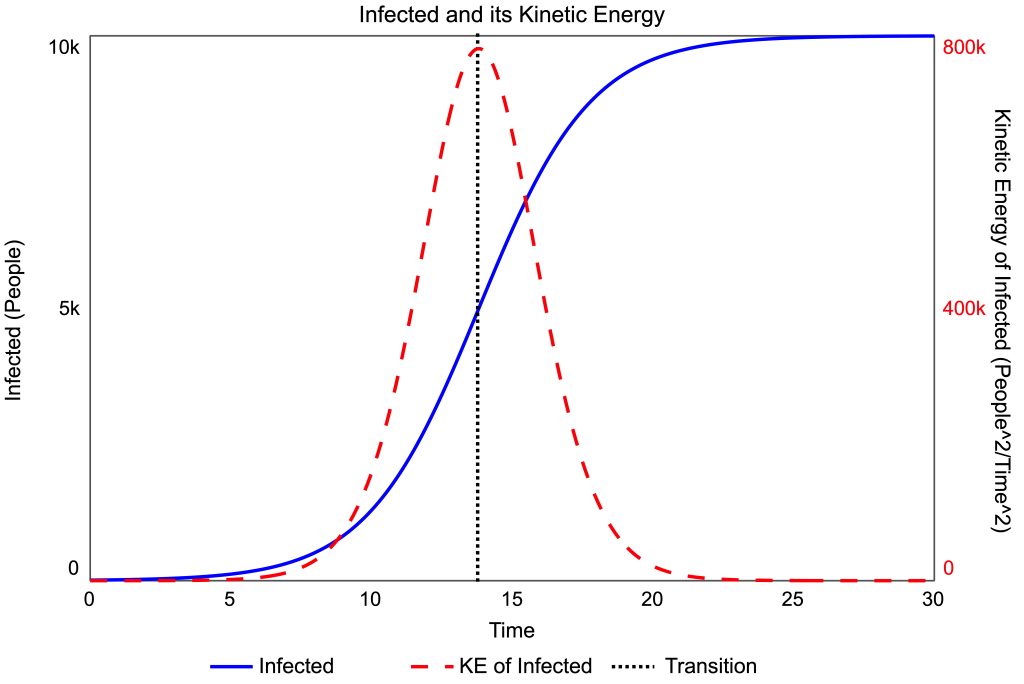
Changes in a stock are measured by its rate of change or flow. Kinetic energy is proportional to the square of the rate of change, just as in mechanics. This kinetic energy measures how fast a stock changes. For example, the kinetic energy of the infected stock rises to a peak at the transition between the loops, and declines afterwards, Figure 2. The first phase is dominated by R1 because it injects more energy than B1 removes, leading to an increase in Infected‘s kinetic energy. After the transition, B1 does more work than R1. Thus, the net effect is that energy is removed from Infected and it slows down, Figure 2.
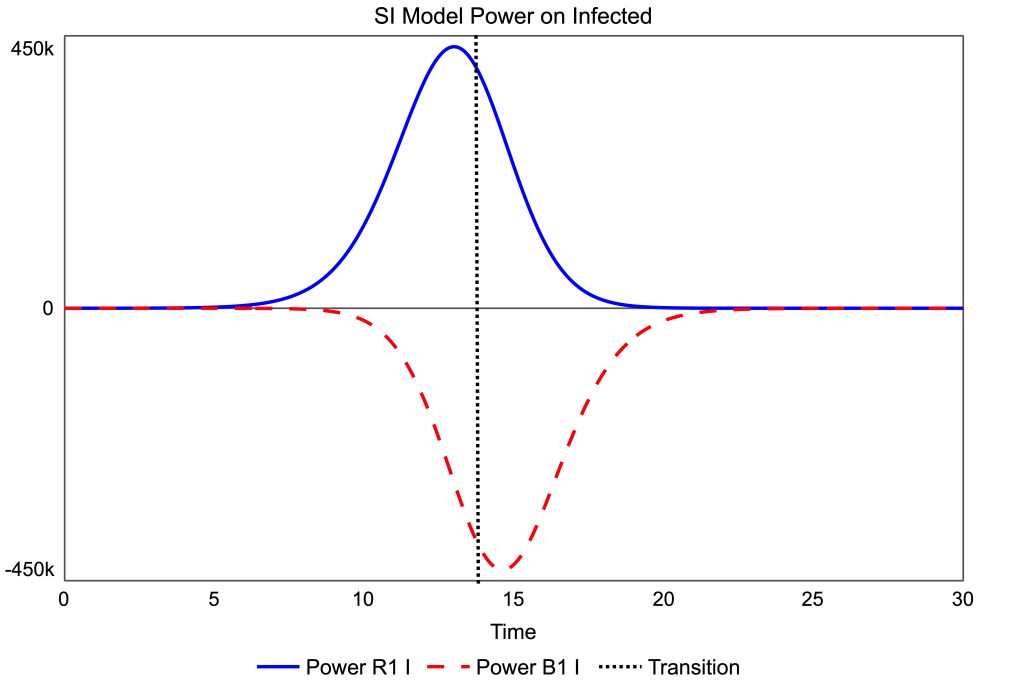
Power
The power of a feedback loop is the rate at which it flows energy into, or out from, a stock. It is derived from force and is proportional to impact. Figure 3 shows R1 imparting energy into the infected stock. It peaks before the transition point. Loop B1 is delayed in removing energy from the stock, hence its kinetic energy increases. The power of B1 peaks after the transition point, Figure 3. The absolute values of the two powers are numerically equal at the transition point.
The energy flows can be placed in the Stock-Flow diagram, Figure 4, illustrating the role of the two loops in the system. In the absence of any other balancing loops, the system only stabilises when all the energy imparted by R1 has been removed by B1, leading to the susceptibles being depleted.

Work Done
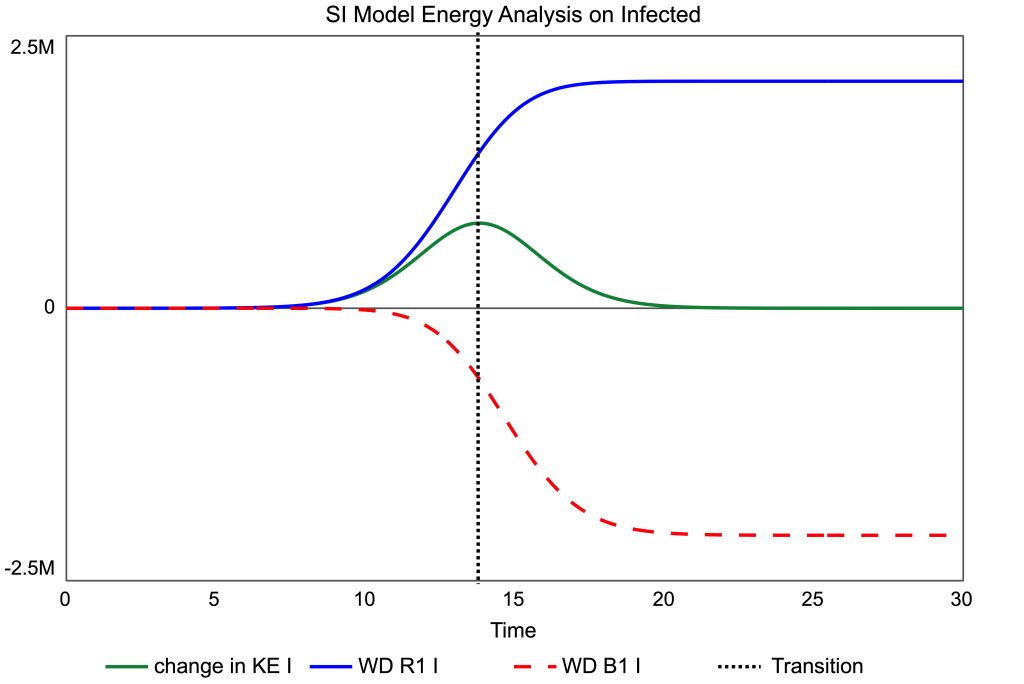
The work done by a feedback loop is an accumulation of the energy it transfers over an interval of time. Figure 5 compares the work done by each loop with the change in kinetic energy of Infected. By the time stability is reached, loop B1 has removed all the energy deposited by R1, time 30. Before that point, R1 has done more work than B1. The excess energy resides in Infected‘s kinetic energy. The peak difference between the two loops is at the transition point. Figure 6 expresses that difference as a bar chart.
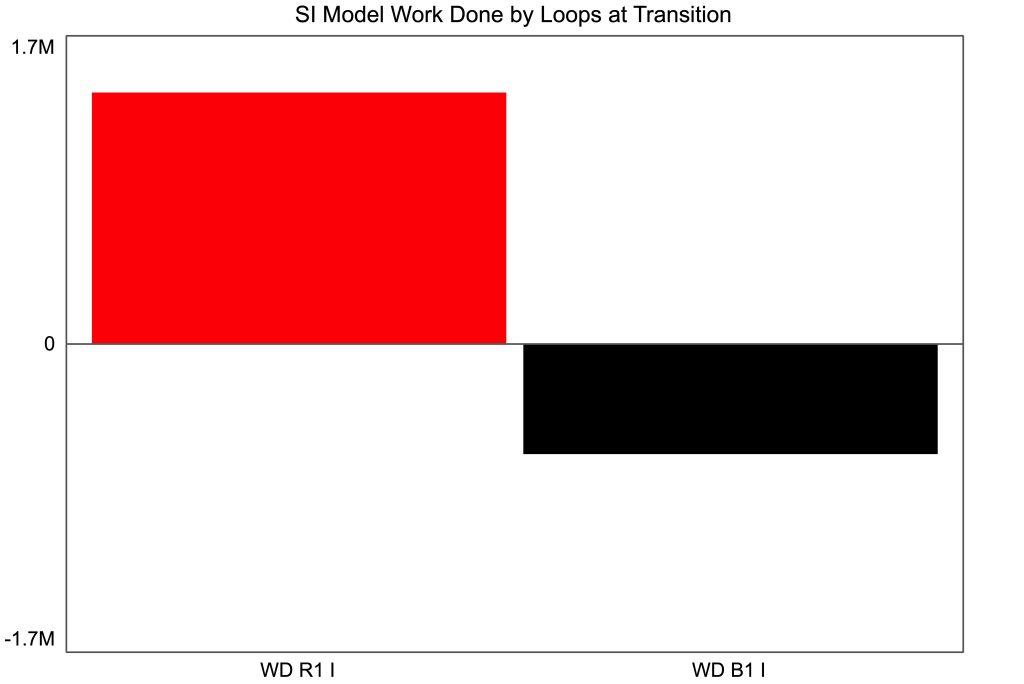
The value of the energy approach lies in its description of the cumulative effect of the loops, rather than an instant-by-instant measurement at each point in time. Stability is attained because the two loops have transferred the same amount of energy, e.g., Figure 6. Work done indicates the purpose of each loop within the context of the entire system.